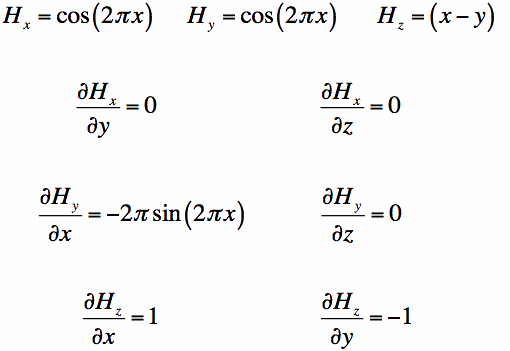The Curl
The Curl Operator
What does the curl operator in the 3rd and 4th Maxwell's Equations mean? What exactly is the meaning of the del symbol with an x next to it, as seen in Equation [1]?
The curl is a measure of the rotation of a vector field. To understand this, we will again use the analogy of flowing water to represent a vector function (or vector field). In Figure 1, we have a vector function (V) and we want to know if the field is rotating at the point D (that is, we want to know if the curl is zero).  Figure 1. Example of a Vector Field Surrounding a Point.
To determine if the field is rotating, imagine a water wheel at the point D. If the vector field representing water flow would rotate the water wheel, then the curl is not zero:
 Figure 2. Example of a Vector Field Surrounding a Water Wheel Producing Rotation.
In Figure 2, we can see that the water wheel would be rotating in the clockwise direction. Hence, this vector field would have a curl at the point D. We must now make things more complicated. Is the curl of Figure 2 positive or negative, and in what direction? Because we are observing the curl that rotates the water wheel in the x-y plane, the direction of the curl is taken to be the z-axis (perpendicular to plane of the water wheel). In addition, the curl follows the right-hand rule: if your thumb points in the +z-direction, then your right hand will curl around the axis in the direction of positive curl. For Figure 2, the curl would be positive if the water wheel spins in a counter clockwise manner. The curl would be negative if the water wheel spins in the clockwise direction. In Figure 2, the water wheel rotates in the clockwise direction. Hence, the z-component of the curl for the vector field in Figure 1 is negative. As you can imagine, the curl has x- and y-components as well. Hence, the curl operates on a vector field and the result is a 3-dimensional vector. That is, if we know a vector field then we can evaluate the curl at any point - and the result will be a vector (representing the x-, y- and z-directions).
Let's do another example with a new twist. Imagine that the vector field F in Figure 3
has z-directed fields. Let the symbol
 Figure 3. A Vector Field With Z-directed Energy - does the Wheel Rotate?.
Will the wheel rotate if the water is flowing up or down around it? The answer is no. Only x- and y- directed vectors can cause the wheel to rotate when the wheel is in the x-y plane. Hence, the z-directed vector fields can be ignored for determining the z-component of the curl. Now, let's take more examples to make sure we understand the curl. What can we say about the curl of the vector field J at point G in Figure 4?
 Figure 4. A Vector Field in the Y-Z Plane.
Is the curl positive, negative or zero in Figure 4? And in what direction is it? First, since the water wheel is in the y-z plane, the direction of the curl (if it is not zero) will be along the x-axis. Now, we want to know whether the curl is positive (counter-clockwise rotation) or if the curl is negative (clockwise rotation). The red vector in Figure 4 is in the +y-direction. However, it will not rotate the water wheel, because it is directed directly at the center of the wheel and won't produce rotation. The green vector in Figure 4 will try to rotate the water wheel in the clockwise direction, but the black vector will try to rotate the water wheel in the counter-clockwise direction - therefore the green vector and the black vector cancel out and produce no rotation. However, the brown vector will rotate the water wheel in the counter clockwise direction. Hence, the net effect of all the vectors in Figure 4 is a counter-clockwise rotation. The result is that the curl in Figure 4 is positive and in the +x-direction. In general, a vector field will have [x, y, z] components. The resulting curl is also a vector with [x, y, z] components. It is difficult to draw 3-D fields with water wheels in all 3-directions but if you understand the above examples you can generalize the 2-D ideas above to 3 dimensions. Now we'll present the full mathematical definition of the curl.
Mathematical Definition of the CurlLet us say we have a vector field, A(x,y,z), and we would like to determine the curl. The vector field A is a 3-dimensional vector (with x-, y- and z- components). That is, we can write A as:
The curl of A is defined to be:
In Equation [3],
The rate of change operators are known as partial derivatives. For more information, see the partial derivative page. As you can see, the curl is very complicated to write out. But the physical meaning can be understood intuitively from the above discussion. In words, Equation [3] says:
So the curl is a measure of the rotation of a field, and to fully define the 3-dimensional rotation we get a 3-dimensional result (the curl in Equation [3]). Let's look at a mathematical example of a vector field and calculate the curl. Suppose we have a vector field H(x,y,z) given by:
Now, to get the curl of H in Equation [6], we need to compute all the partial derivatives below:
Using the results of Equation [7] into the curl definition of Equation [3] gives the curl of H:
So we have the curl of H in Equation [8]. Note that the curl of H is also a vector function. As such, we can say that a new vector (we'll call it V) is the curl of H. Hence, V can be evaluated at any point in space (x,y,z). For instance, the x-component of V will always have Vx=-1. Similarly, Vy=-1. But Vz depends on x. Hence, V(3,4,0) will have Vz=0, but V(3,4, 0.5) will have Vz = 2*pi. This gives about all the information you need to know about the curl. The important points to remember are that the curl operates on a vector function, and returns a vector function. The resulting curl is a measure of the rotation of the field in the 3 principal axis (x-, y-, z-).
|
represent a vector in the +z-direction
and the symbol 
represent a vector in the -z direction:
is a unit vector in the +x-direction, 
is a unit vector in the +y-direction, and 
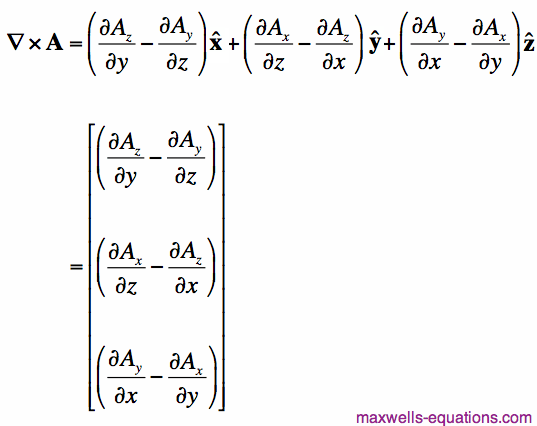
is a unit vector in the +z-direction
(a unit vector is a vector with a magnitude equal to 1). The terms such as:
