Gauss' Law for Magnetism

Gauss' Law for Magnetic Fields Before you read this page, you should have read the page on Gauss' Law for Electric Fields. If that makes sense, then the second of Maxwell's Equations will be pretty easy. First, observe both of Gauss' Laws, written in Equation [1]: [Equation 1] You see that both of these equations specify the divergence of the field in question. For the top equation, we know that Gauss' Law for Electric Fields states that the divergence of the Electric Flux Density D is equal to the volume electric charge density. But the second equation, Gauss' Magnetism law states that the divergence of the Magnetic Flux Density (B) is zero. Why? Why isn't the divergence of B equal to the magnetic charge density? Well - it is. But it just so happens that no one has ever found magnetic charge - not in a laboratory or on the street or on the subway. And therefore, until this hypothetical magnetic charge is found, we set the right side of Gauss' Law for Magnetic Fields to zero: 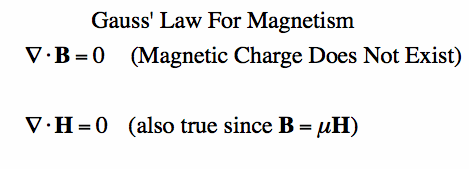Since B and the Magnetic Field H are related by the permeability , we note in Equation [2] that the divergence of the magnetic field is also zero. Now, you may have played with magnets when you were little, and these magnetic objects attracted other magnets similar to how electric charges repel or attrach like electric charges. However, there is something special about these magnets - they always have a positive and negative end. This means every magnetic object is a magnetic dipole, with a north and south pole. No matter how many times you break the magnetic in half, it will just form more magnetic dipoles. Gauss' Law for Magnetism states that magnetic monopoles do not exist - or at least we haven't found them yet. Because we know that the divergence of the Magnetic Flux Density is always zero, we now know a little bit about how these fields behave. I'll present a couple of examples of legal and illegal Magnetic Fields, which are a consequence of Gauss' Law for Magnetism: 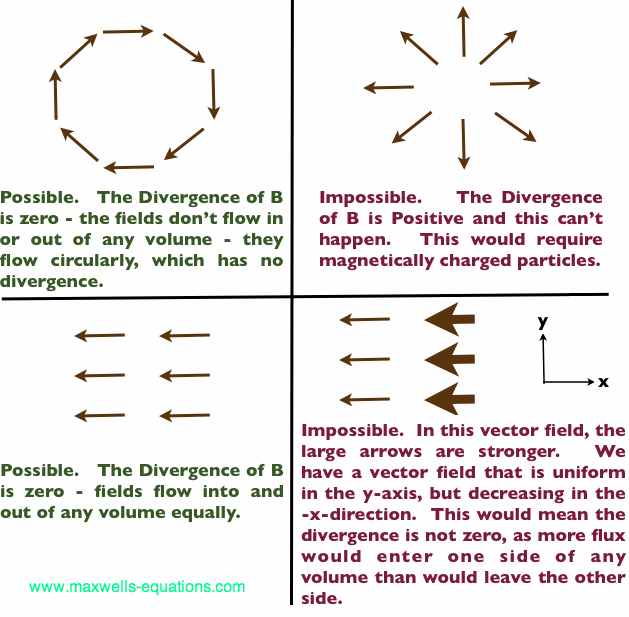Figure 1. Example of Possible and Impossible Magnetic Field Distributions. In summary, the second of Maxwell's Equations - Gauss' Law For Magnetism - means that: Magnetic Monopoles Do Not Exist The Divergence of the B or H Fields is Always Zero Through Any Volume Away from Magnetic Dipoles, Magnetic Fields flow in a closed loop. This is true even for plane waves, which just so happen to have an infinite radius loop. There you have it - Gauss' Law for Magnetic Fields. If you understood Gauss' Law for Electric Fields, this isn't very complicated. Maxwell's Equations This page on the second of Maxwell's Equations (Gauss' Law for Magnetic Fields) is copyrighted. Please don't reproduce without permission. Copyright maxwells-equations.com, 2012.