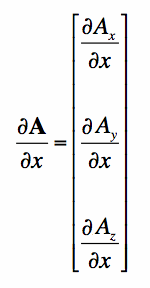The Partial Derivative

The Partial Derivative Suppose we have a function of 3-variables: f(x,y,z). Then the partial derivative of f with respect to x is writen: [Equation 1] The partial derivative means the rate of change. That is, Equation [1] means that the rate of change of f(x,y,z) with respect to x is itself a new function, which we call g(x,y,z). By "the rate of change with respect to x" we mean that if we observe the function at any point, we want to know how quickly the function f changes if we move in the +x-direction. To give a loose but concrete example, let's say f is a linear or slowly varying function. Assume f(0,0,0)=3, and that f(1,0,0)=5. Then we would say that the rate of change of f in the +x-direction, evaluated at (0,0,0) is +2. This is because the function f increased by 2 over a span of x=1. This is the rate of change of f with respect to x. Finally, the rate of change can be positive, negative or zero. To give a little more rigor or if the above is unclear, we'll define (ordinary) derivatives and then look at the derivatives of vector functions. Derivatives In this page, we'll simplify things and discuss ordinary derivatives. This is simpler because we look at single variable functions. If we have a function p(x), then the derivative of p with respect to x is written: [Equation 2] The derivative of p(x) is another function, which we write as q(x). As an example, let's look at some simple functions. The first, is p(x)=3. The functions p(x) and hte derivative q(x) are plotted in Figure 1: 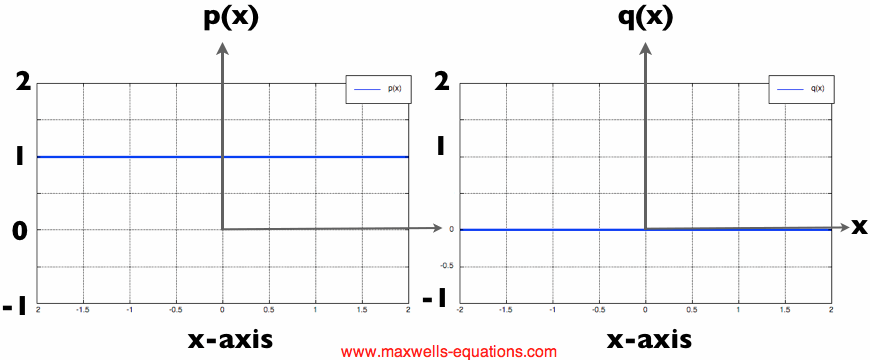Figure 1. The constant function (left) and its derivative (right). Does Figure 1 make sense to you? On the left in Figure 1 we have the constant function p(x). Note that p does not change at all. Hence, the rate of change (the derivative of p) should be zero (no change). And this is exactly what we get, the right graph in Figure 1. When that makes sense, let's look at a slightly more complicated example, p(x)=x. This is a simple linear function, and is shown with its derivative in Figure 2: 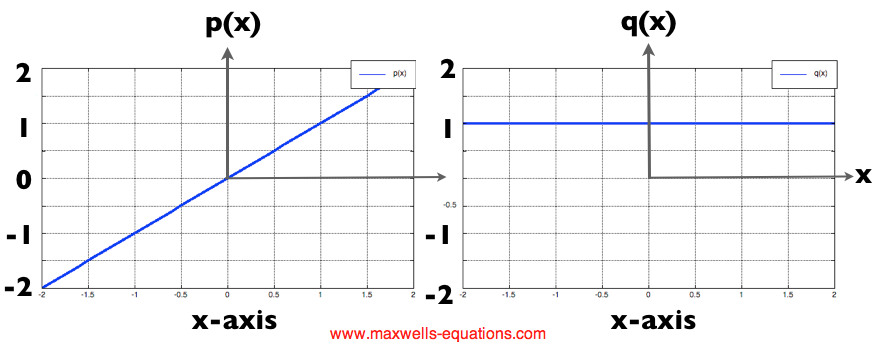Figure 2. A linear function (left) and its derivative (right). Again you should ask yourself if q(x) is the correct derivative. Is it? Here we have a function that is increasing at a constant rate - a linearly increasing function. This means that the function is always changing at the same rate - so the derivative should be a constant. And q(x)=1, which is a constant. So this is right. Make sense? Let's do a 3rd example that is again slightly more complicated - a quadratic function: 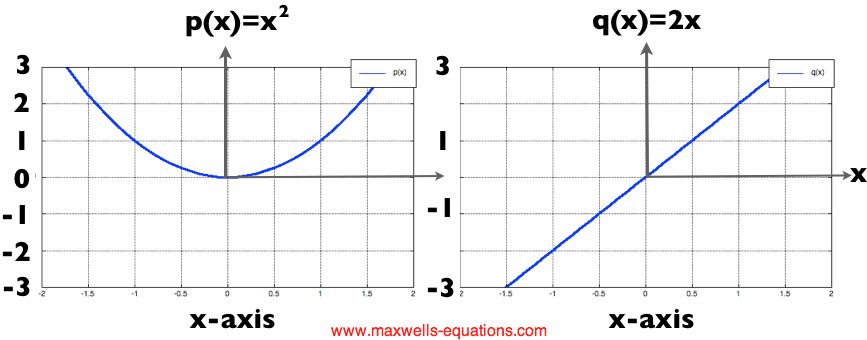Figure 3. A quadratic function (left) and its derivative (right). If you can understand Figure 3 and you've never seen derivatives before, you have good intuition. The quadratic function p is decreasing for x less than zero. Exactly at x=0, the function is actually not changing - for an instant, as it switches from decreasing to increasing in a smooth fashion. Finally, above x equals zero, the function p is increasing. In addition, the rate that p is increasing also increases as x increases - the slope gets more and more steep. This produces the derivative of p, the right side of Figure 3. The derivative q is a linear function 2*x. This means the rate of change of p is continuously increasing. Does that make sense? It's a tough concept but you should stare at it until it makes sense if you want to understand derivatives. Back to Partial Derivatives When we go back to multivariable functions - that is, we look at f(x,y,z) instead of f(x), then determining the partial derivative is only mildly more complicated. The mathematical fact of the matter is that if we are taking the derivative with respect to x, then we can treat the other variables (y and z) as constants. That is, we can essentially treat them the way we would any number, like +5 or -3. The reason is that the partial derivative of f with respect to x should only be looking at what happens to f when x changes slightly, and the others are held constant. As a quick example, let's evaluate the partial derivative of f(x,y,z) with respect to y for the function in Equation [3]. I use a little calculus, but we hold the variables x and z constant and we get: [Equation 3] Partial Derivatives of Vector Functions The derivative can also be applied to vector functions in a very natural form. For Maxwell's Equations, we use 3-dimensional vector functions. So if we have a vector function A in Equation [4]: [Equation 4] The partial derivative of A with respect to x is then simply the partial derivative of each of the components individually: [Equation 5] Equation [5] shows that the partial derivative of a vector function is the natural extension of the partial derivative of a scalar function. And this should give you all the information you need to know about partial derivatives that you'll need to know for Maxwell's Equations. Maxwell's Equations This page on the partial derivatives and ordinary derivatives is copyrighted, particularly the application of it to Maxwell's Equations. The copyright belongs to Maxwells-Equations.com, 2012.