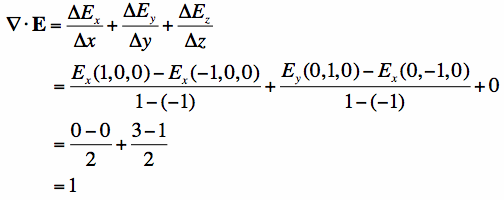Divergence

The Divergence Operator What does the symbol in Equation 1 mean? What is an upside-down triangle (also known as the del operator) with a dot next to it do? [Equation 1] In this section, I'll give the definition with no math: Divergence at a point (x,y,z) is the measure of the vector flow out of a surface surrounding that point. That is, imagine a vector field represents water flow. Then if the divergence is a positive number, this means water is flowing out of the point (like a water spout - this location is considered a source). If the divergence is a negative number, then water is flowing into the point (like a water drain - this location is known as a sink). I will give some examples to make this more clear. First, imagine we have a vector field (given by the vector function A) as shown in Figure 1, and we want to know what the divergence is at the point P: Figure 1. Example of a Vector Field Surrounding a Point. We also draw an imaginary surface (S) surrounding the point P. Now imagine the vector A represents water flow. Then, if you add up the amount of water flowing out of the surface, would the amount be positive? The answer, is yes: water is flowing out of the surface at every location along the surface S. Hence, we can say that the divergence at P is positive. Let's take another simple example, that of Figure 2. We have a new vector field B surrounding the point P: Figure 2. Example of a Vector Field Surrounding a Point (negative divergence). In Figure 2, if we imagine the water flowing, we would see the point P acting like a drain or water sink. In this case, the flow out of the surface is negative - hence, the divergence of the field B at P is negative. Pretty simple, eh? Here's a couple more examples. Figure 3 has a vector field C surrounding the point: Figure 3. Example of a Vector Field with no Variation around a Point. In Figure 3, if C represents the flow of water, does more water flow into or out of the surface? In the top of Figure 3, water flows out of the surface, but at the bottom it flows in. Since the field has equal flow into and out of the surface S, the divergence is zero. Seeing as you are probably having a great time, let's do two more examples. Check out Figure 4: Figure 4. A field that wraps around a Point. In Figure 4, we have a vector field D that wraps around the point P. Is the flow positive (out of the surface) or negative (into the surface)? At each point along the surface S, the field is flowing tangentially along the surface. Therefore the field is not flowing into or out of the surface at each point. Hence, again, we have the divergence of D equal to 0 at P. Let's look at a last example, the field E in Figure 5: Figure 5. A More Complicated Vector Field around a point. The vector field E has a large vector above the point P indicating a strong field there - a lot of water flowing out of the surface. The vector to the left of P is small and tangential to the surface, so there is no flow into or out of S at that point. The same is true for the vector to the right of P. And the vector below P is small, indicating a smaller amount of water flowing into the surface. Hence, we can guess the divergence is positive - more water is flowing out of the surface than into it. But how exactly is divergence quantified? To get to that, we'll have to move on to the mathematical section of the divergence page. The Math Behind the Divergence First, we must know that the divergence operator can only accept a vector function as an input. A vector function is simply a vector of 3-functions, broken into x-, y-, and z- components. To learn more, see the vector function page. Divergence is a specific measure of how fast the vector field is changing in the x, y, and z directions. If a vector function A is given by: [Equation 2] Then the divergence of A is the sum of how fast the vector function is changing: [Equation 3] The symbol is the partial derivative symbol, which means rate of change with respect to x. For more information, see the partial derivatives page. Divergence Mathematical Examples Let's recall the vector field E from Figure 5, but this time we will assign some values to the vectors, as shown in Figure 6: Figure 6. The Vector Field E with Vector Magnitudes Shown. In Figure 6, let's assume that E is not changing in the z-direction, so that we can neglect the final term in Equation [3]. We will also assume that over this region (around point P) that everything is varying linearly. Then what is the divergence in Figure 6? Using Equation [3], we can estimate the rate of change in the x and y-directions (assuming the rate of change in z is zero): [Equation 4] You should make sure Equation [4] makes sense. Note that when we evaluate the x-rate of change of E, we only care about the Ex component. If you look at the blue vectors in Figure 6, you can see that at locations (1,0,0) and (-1,0,0) we have Ex=0. Hence there is no change of Ex in x. However, if you look at the rate of change of E in the y-direction, we have Ey=3 at (0,1,0) and Ey=1 at (0,-1,0). Therefore, there is more flow out of the point P than into the point with respect to the y-direction. Hence the point P acts as a source, and the divergence is positive. Let us now move on to Example 2. I will assume you know a little bit of calculus, so that I can use the derivative operation. The derivative (as shown in Equation [3]) calculates the rate of change of a function with respect to a single variable. Consider the vector function A in Equation [5]: [Equation 5] The divergence can be calculated using Equation [3]: [Equation 6] Equation [6] gives us the divergence at every location in space. That is, if you want to know the divergence at (x,y,z)=(3,2,1) then we can use equation [6] to see that the divergence of A is 2+6*1 = 8. We can find the divergence at any point in space because we knew the functions defining the vector A from Equation [5], and then calculated the rate of changes (derivatives) in Equation [6]. I think this pretty well sums up divergence, at least as far as we will need to know for Maxwell's Equations. Remember: for any point in space, the divergence takes a vector function and produces a single number. This number evaluates whether the point acts as a source of fields (produces more fields than it takes in) or as a sink of fields (fields are diminished around the point). Maxwell's Equations This page on divergence (div operator) is copyrighted, particularly the application to Maxwell's Equations. No portion can be reproduced except by permission of the author. Copyright Maxwells-Equations.com, 2012.