Forms of Maxwell's Equations

Maxwell's Equations are commonly written in a few different ways. The form we have on the front of this website is known as point form: 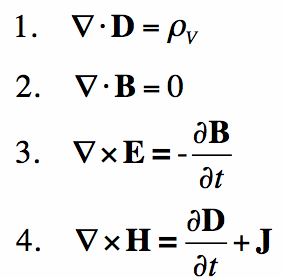The above equations are known as "point form" because each equality is true at every point in space. However, if we integrate the point form over a volume, we obtain the integral form. There is also Time-Harmonic Form, and Maxwell's Equations written only with E and H. And one form uses imaginary magnetic charge, which can be useful for some problem solving. We discuss these below. Integral Form of Maxwell's Equations If the point form of Maxwell's Equations are true at every point, then we can integrate them over any volume (V) or through any surface and they will still be true. There are a couple of Vector Calculus Tricks listed in Equation [1]. [Equation 1] I won't go through the derivation, but you use the divergence theorem on the first two of Maxwell's Equations (Gauss' Laws) and integrate through a volume V with boundary surface (S). You use Stokes' Theorem on Faraday's and Ampere's Law on an open surface (S) with a boundary line (L). The result is below: 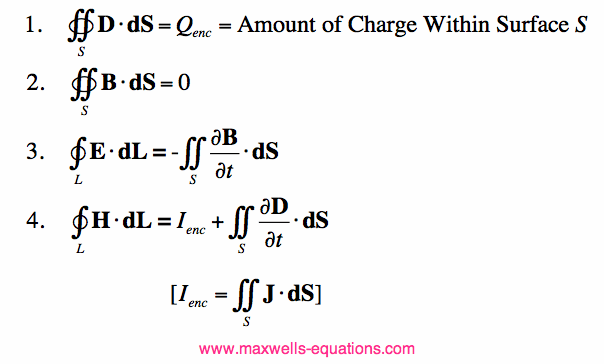Maxwell's Equations in Integral Form. Note that in the first two equations, the surface S is a closed surface (like the surface of a sphere), which means it encloses a 3D volume. In the last two equations, the surface S is an open surface (like a circle), that has a boundary line L (the perimeter of the open or non-closed surface). Time-Harmonic Form of Maxwell's Equations We know from the theory of Fourier Transforms that every signal in time can be rewritten as the sum of sinusoids (sign or cosine). Using a little more complex math and we can specify the time variation in terms of the sum of sinusoids written in complex form: [Equation 2] In Equation [2], f is the frequency we are interested in, which is equal to . Hence, the time derivative of the function in Equation [2] is the same as the original function multiplied by . This means we can replace the time-derivatives in the point-form of Maxwell's Equations [1] as in the following: Maxwell's Equations in Time-Harmonic Form. This is known as phasor form or the time-harmonic form of Maxwell's Equations. It is perfectly legitimate, because this form tells us how the waves behave if they are oscillating at frequency f, and all waves can be decomposed into the sum of simple oscillating waves. Maxwell's Equations Written Only with E and H We can also rewrite Maxwell's Equations with only E and H present. This means we are going to get rid of D, B and the Electric Current Density J. We can do this by using the equations: [Equation 3] If we substitute these into Equation [1], we can obtain Maxwell's Equations with only Electric and Magnetic Fields: 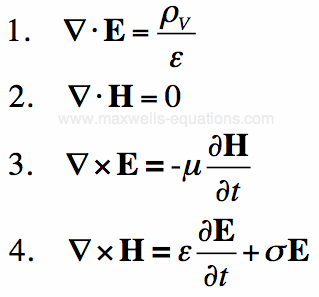Maxwell's Equations Written With only E and H. Symmetric Form of Maxwell's Equations - with Magnetic Charge What if someone finds Magnetic Monopoles? Then we'd have to alter Maxwell's Equations. And then we would also have to alter the equations to allow for Magnetic Current (i.e. the flow of Magnetic Charge). This isn't a purely abstract exercise - some problems in Engineering can be solved more simply by assuming a given field distribution is actually a fictitious magnetic charge or magnetic current - it makes the solution easier. So you may also come across the following form of Maxwell's Equations, but you should know that some of the terms don't exist in reality: Maxwell's Equations Written With Magnetic Charge and Magnetic Current. As you can see, we've introduced the magnetic volume charge density to the second Equation, and magnetic current density to the third Equation. Maxwell's Equations This page on the forms of Maxwell's Equations is copyrighted. No portion can be reproduced except with permission. The copyright belongs to Maxwells-Equations.com, 2012.