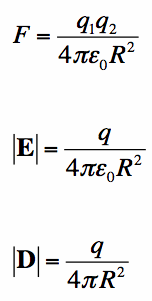Gauss' Law
Gauss' Law
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
In Equation [1], the symbol
Equation [1] is known as Gauss' Law in point form. That is, Equation [1] is true at any point in space. That is, if there exists electric charge somewhere, then the divergence of D at that point is nonzero, otherwise it is equal to zero. To get some more intuition on Gauss' Law, let's look at Gauss' Law in integral form. To do this, we assume some arbitrary volume (we'll call it V) which has a boundary (which is written S). Then integrating Equation [1] over the volume V gives Gauss' Law in integral form:
I probably made things less clear, but let's go through it real quick. As an example, look at Figure 1. We have a volume V, which is the cube. The surface S is the boundary of the cube (i.e. the 6 flat faces that form the boundary of the volume). 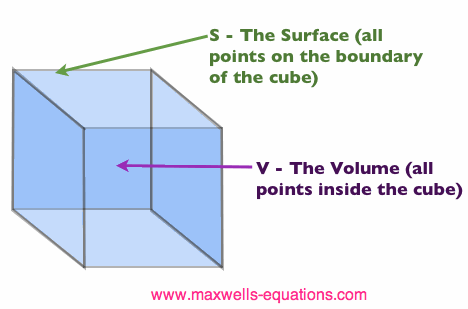 Figure 1. Illustration of a volume V with boundary surface S.
Equation [2] states that the amount of charge inside a volume V
(=
An example with the cube in Figure 1 might help make this clear. Look at the point P in Figure 2, where we have drawn the D field vector:  Figure 2. The D Field on the Surface Can be Broken Down into Tangential (Dt) and Normal (Dn) Components.
We can rewrite any field in terms of its tangential and normal components, as shown in Figure 2. From Equation [3], we are only interested in the component of D normal (orthogonal or perpendicular) to the surface S. We write this as Dn. The tangential component Dt flows along the surface. If you imagine the D field as a water flow, then only the component Dn would contribute to water actually leaving the volume - Dt is just water flowing around the surface. Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume). Interpretation of Gauss' LawWhat does this matter? Gauss' Law states that electric charge acts as sources or sinks for Electric Fields. If you use the water analogy again, positive charge gives rise to flow out of a volume - this means positive electric charge is like a source (a faucet - pumping water into a region). Conversely, negative charge gives rise to flow into a volume - this means negative charge acts like a sink (fields flow into a region and terminate on the charge). This gives us a lot of intuition about the way fields can physically act in any scenario. For instance, here are possible and impossible situations for the Electric Field, as decided by the universe in the Law of Gauss it setup:
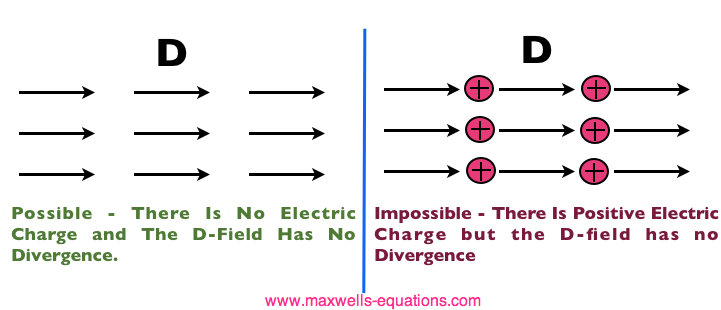 Figure 3. Example #1 of Gauss' Law: The D Field Must Have the Correct Divergence.
 Figure 4. Example #2 of Gauss' Law: The Charges Dictate the Divergence of D .
 Figure 5. Example #3 of Gauss' Law: Negative Charge Indicates the Divergence of D should be negative.
If you observe the way the D field must behave around charge, you may notice that Gauss' Law then is equivalent to the Force Equation for charges, which gives rise to the E field equation for point charges:
Equation [4] shows that charges exert a force on them, which means there exists E-fields that are away from positive charge and towards negative charge. This means opposite charges attract and negative charges repel. And since D and E are related by permittivity, we see that Gauss' Law is a more formal statement of the force equation for electric charges. In summary, Gauss' Law means the following is true: And there you go! If you understand the above statements you understand Gauss' Law, probably better than the mathematicians who invent super complicated math to explain physical phenomena! Intuition trumps complication, always.
|

 is the
is the

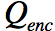 ) is equal to the total amount of
Electric Flux (D) exiting the surface S. That is, to determine
the Electric Flux leaving the region V, we only need to know how
much electric charge is within the volume. We rewrite Equation [2] with
more of the terms defined in Equation [3]:
) is equal to the total amount of
Electric Flux (D) exiting the surface S. That is, to determine
the Electric Flux leaving the region V, we only need to know how
much electric charge is within the volume. We rewrite Equation [2] with
more of the terms defined in Equation [3]: